Cerita Bebas

A Wonderful Night


Acara ini mungkin sudah pernah ditayangkan di tv dan saya pernah menontonnya .
saya suka sama film film streetball , karena menurut saya itu keren bisa menunjukan skill atau kemampuan kita .
Acaranya itu adalah L.A Lights Streetball dan itu setahun sekali , dan saya baru pertama kali nonton secara langsung di senayan tanggal 22 oktober 2011 . Saya datang dengan teman-teman dan berangkat jam 3 sore sampai sana jam 4. Tempatnya aja buat saya udah keren , tapi sayangnya saya kurang begitu nyaman disana karna banyak sekali asap rokok. Mungkin disebabkan sponsor rokoknya juga . Pas saya sampai disana , udah mulai rame dan ada stasiun tv juga datang kesana . Saking ramenya saya susah liat jalan pertandingan tersebut.
Tapi acara intinya itu malam, karna ada pemain All Star NBA. Semua pengunjung semakin banyak dan membuat kemacetan yang parah. Saya terpaksa nonton di luar dan untungnya di luar dikasih layar supaya penonton yang tidak kebagian di dalam bisa melihat pertandingannya dari luar. Saya benar-benar menikmati acara tersebut sampai malam, karna para pemainnya keren-keren terutama di skillnya dan para penonton semua teriak ketika ada moment para pemainnya menunjukkan skillnya. Sekitar jam 12 malam saya baru pulang dan sampai rumah jam 1 malam. Badan saya serasa capek sekali habis menonton acara itu, tapi semua rasa capeknya hilang saat saya masuk kamar. Karena ternyata orang tua saya memberikan surprise kepada saya. Mereka membelikan sebuah gitar baru untuk saya. Saya merasa saat itu malam yang sangat indah dan bahagia buat saya. I will never forget that moment in my life...

Relasi

Relasi, dalam matematika, adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.

DEFINISI

 

Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari Ake B adalah subhimpunan dari A×B.

 RELASI DAN FUNGSI PROPOSISI

 

Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunan W = { hijau, kuning, orange}. Suatu relasi R dari A ke B didefinisikan sebagai R= {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisi w(x, y) = "x berwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.

 RELASI A×A

Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:

• Refleksif
• Irefleksif
• Simetrik
• Anti-simetrik
• Transitif

Kita menyebut relasi R dari A kepada A sebagai relasi R dalam A.

Relasi Refleksif

Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen Aberhubungan dengan dirinya sendiri.

atau

Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan xdan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.

 Relasi Irefleksif

Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.

atau

Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.

 Relasi Simetrik

Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota Aberhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.

atau

Sebuah relasi “x + y genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.

Relasi Anti-simetrik

Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsia dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.

atau

Dalam kebanyakan literatur biasanya ditulis sebagai kontraposisinya seperti di bawah ini. Keuntungan bentuk ini adalah tidak mengandung negasi, dan hanya mengandung satu implikasi.

atau

Relasi  bersifat anti-simetrik, karena  mengakibatkan . Demikian juga jika ada p dan q yang terhadap mereka berlaku 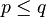 dan 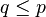 berarti p = q.

 Relasi Transitif

Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan bberhubungan dengan c, maka a berhubungan dengan c secara langsung.

atau

Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7.

RELASI KHUSUS

Relasi Ekivalen

Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:

• Refleksif
• Simetrik, dan
• Transitif

Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.

 Orde Parsial

Orde parsial adalah relasi yang bersifat:

• Refleksif
• Anti-simetrik, dan
• Transitif

Suatu relasi dari himpunan A ke himpunan B adalah pemasangan atau perkawanan atau korespondensi dari anggota-anggota himpunan A ke anggota-anggota himpunan B.

Jika diketahui himpunan A = {0, 1, 2, 5}; B = {1, 2, 3, 4, 6}, maka relasi “satu kurangnya dari” himpunan A ke himpunan B dapat disajikan dalam diagram panah, diagram Cartesius, himpunan pasangan berurutan, dan dengan rumus.

Relasi dari himpunan A ke himpunan B adalah aturan yang memasangkan anggota himpunan A dan anggota himpunan B dengan aturan tertentu.


Kali ini, diperkenalkan 4 cara menyatakan relasi, yaitu:

1. Dengan Himpunan Pasangan Berurutan

2. Dengan Diagram Panah

3. Dengan Diagram Cartesius

4. Dengan Rumus

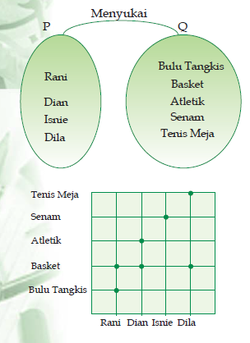
1.  Diagram Panah

Anggota-anggota himpunan P berelasi dengan anggota himpunan Q dengan relasi “menyukai”. Hal tersebut ditunjukkan dengan arah panah. Oleh karena itu, diagramnya disebut diagram panah.

2.  Diagram Kartesius

Diagram kartesius merupakan diagram yang terdiri atas sumbu X dan sumbu Y. Pada diagram kartesius, anggota himpunan P terletak pada sumbu mendatar (sumbu-X), sedangkan anggota himpunan Q terletak pada sumbu tegak (sumbu-Y). Relasi yang menghubungkan himpunan P dan Q ditunjukkan dengan noktah atau titik sepertiterlihat pada gambar.



3.  Himpunan Pasangan Berurutan

Selain menggunakan diagram panah dan kartesius, sebuah relasi yang menghubungkan himpunan yang satu dengan himpunan lainnya dapat disajikan dalam bentuk himpunan pasangan berurutan. Adapun cara penulisannya adalah anggota himpunan P ditulis pertama, sedangkan anggota himpunan Q menjadi pasangannya.

Berdasarkan soal di atas, maka diperoleh himpunan pasangan berurutan sebagai berikut.

{(Rani, basket), (Rani, bulu tangkis), (Dian, basket), (Dian, atletik), (Isnie, senam), (Dila, basket), (Dila, tenis meja)}

4. Dengan Rumus

f(x) = x + 1, di mana x = {0, 1, 2, 5} dan f(x) = {1, 2, 3, 4, 6}

Relasi Invers
Setiap Relasi dari A ke B, mempunyai relasi R-1 dari B ke A yang didefinisikan sebagai
R-1 = {(b,a) ½ (a,b) Î R}
contoh:
A = {1,2,3}; B = {a,b}
R = {(1,a), (1,b), (3,a)} relasi dari A ke B
R-1 = {(a,1), (b,1), (a,3)} relasi invers dari B ke A

DOMAIN DAN RANGE
Domain (daerah asal) dari suatu relasi R adalah himpunan elemen pertama dari pasangan berurutan elemen R.
Domain = { a ½ a Î A, (a,b) Î R }
Range (daerah hasil) dari suatu relasi R adalah himpunan elemen kedua dari pasangan berurutan elemen R.
Range = {b ½ b Î B, (a,b) Î R}
contoh:
A = {1,2,3,4} ; B = {a,b,c}
R = {(2,a) ; (4,a) ; (4,c)}
Domain = {2,4}
Range = {a,c}

Komposisi  Relasi

Komposisi relasi seperti halnya komposisi fungsi jadi seperti  kombinasi hanya beda macam operasinya.

Misal R adalah relasi dari himpunan A ke himpunan B, dan S adalah relasi dari himpunan B ke himpunan C. komposisi R dan S dinotasikan dengan  R₀S adalah relasi dari A ke C yang didefinisikan oleh

          R₀S = {(a,c)|aЄA, c Є C, dan untuk beberapa bЄB, (a,b)ЄR dan (b,c)ЄS}

Sifat-sifat relasi biner

1. Refleksif

Relasi R pada himpunan A disebut refleksif,  jika (a,a)ЄR untuk setiap aЄA.

2. Simetris (setangkup)

Sebaliknya dikatakan tidak simetris.

Contoh

Relasi R didefinisikan pada himpunan A dimana  A={1,2,3,4}

a) Diketahui ,  R={(1,1), (1,2),(2,1), (2,2), (2,4), (4,2), (4,4)}

b) Diketahui , R={(1,1),  (2,3), (4,2), (4,3), (4,4)}.

Tentukan apakah R simetris ?

Jawab

a) simetris karena jika (a,b)ЄR, ada juga  (b,a)ЄR yaitu (1,2) , (2,1) ЄR, begitu juga (2,4) , (4,2)ЄR

b) tidak simetris karena (2,3)ЄR tetapi (3,2) tidak dalam R

Dilihat cara penulisan relasi, relasi bersifat simetris mempunyai matriks yang elemen-elemen dibawah diagonal utama merupakan pencerminan dari elemen-elemen diatas diagonal utama, atau m_ij = m_ji umtuk i= 1,2,.......n. sedangkan graf berarahnya mempunyai ciri : jika ada busur a ke b, maka ada juga busur dari b ke a

3. Transitif (penghantar)

Relasi R pada himpunan A disebut  transitif (penghantaf), untuk a, b, c Є A, jika (a,b)ЄR dan (b,c)ЄR,maka harus ada (a,c)ЄR.

LATIHAN SOAL

1. A = {Buyung, Doni, Vita, Putri}, B = {IPS, kesenian, keterampilan, olahraga, matematika, IPA, bahasa Inggris}, dan “pelajaran yang disukai” adalah relasi yang menghubungkan himpunan A ke himpunan B.

keterangan: Buyung suka IPS dan kesenian, Doni suka Ketrampilan dan Olahraga, Vita suka IPA, dan Putri suka Matematika dan Bahasa Inggris.

Jawaban dengan tiga metode:

a. Dengan metode diagram panah

b. Dengan metode diagram Cartesius

c. Dengan metode himpunan pasangan berurutan

{(Buyung, IPS), (Buyung, kesenian), (Doni, keterampilan), (Doni, olahraga), (Vita, IPA), (Putri, matematika), (Putri, bahasa Inggris)}

2. Relasi R didefinisikan pada himpunan A dimana  A={1,2,3,4}

a) Diketahui ,  R={(1,1), (1,3),(2,1), (2,2), (3,3), (4,2), (4,3), (4,4)}

b) Diketahui , R={(1,1),  (2,2), (2,3), (4,2), (4,3), (4,4)}.

Tentukan apakah R refleksif ?

Jawab

a) bersifat refleksif karena  (a,a) ada dalam R yaitu (1,1), (2,2), (3,3), dan (4,4)

b) tidak refleksif karena ada (a,a) tidak ada dalam R yaitu (3,3).

Dilihat dari cara penulisan relasi, relasi yang bersifat refleksif mempunyai matriks denganbentuk semua bernilai 1 pada diagonal utamanya ,  sedangkan graf berarah adanya gelang pada setiap simpulnya.

3. A={1,2,3,4}, dan relasi R pada A

a) diketahui R= {(2,1), (3,1),(3,2), (4,1), (4,2), (4,3)}

b) Diketahui , R={(1,1),  (2,3),  (2,4), (4,2)}.

Tentukan apakah R refleksif ?

Jawab

a) transitif karena memenuhi syarat untuk, a,b,c ЄA, jika ada (a,b)ЄR dan (b,c)ЄR,maka terlihat ada (a,c)ЄR.

b) tidak bersifat transitif karena tidak memenuhi syarat untuk, a,b,c ЄA, jika ada (a,b)ЄR dan (b,c)ЄR,tidak terlihat ada (a,c)ЄR. Dalam hal ini ada (2,4), dan(4,2) tetapi (2,2)ÏR

Sumber : http://oestadnetral.blogspot.com/2012/11/relasi.html

http://indahkwardani.wordpress.com/2014/05/06/relasi/

http://cabangmatematika.blogspot.com/2014/02/pengertian-relasi-beserta-contoh-soal.html

http://matkdimasfun.blogspot.com/2011/12/relasi-dan-fungsi.html

http://dianitaawulan.wordpress.com/2013/06/14/matriks-relasi-dan-diagram-panah-relasi-invers/

http://relasidanfungsi.weebly.com/macam-macam-penyajian-relasi.html

HIMPUNAN

1. Pengertian Himpunan

Himpunan diperkenalkan oleh George Cantor (1845 – 1918), seorang ahli matematika Jerman. Ia menyatakan bahwa himpunan adalah kumpulan atas objek-objek. Objek tersebut dapat berupa benda abstrak maupun kongkret. Pada dasarnya benda-benda dalam suatu himpunan tidak harus mempunyai kesamaan sifat/karakter. 

Kumpulan dari sebatang pensil, sebuah kursi dan setangkai bunga membentuk sebuah himpunan. Ketiga benda tersebut berupa benda kongkret, namun tidak memiliki kesamaan sifat. Benda-benda dalam suatu himpunan harus terdefinisi dengan jelas, well defined, artinya dapat dibedakan apakah suatu benda termasuk ataupun tidak dalam himpunan tersebut. Sebagai contoh, kumpulan semua bilangan genap membentuk sebuah himpunan, sebab syarat keanggotaannya terdefinisi dengan jelas.

Kumpulan orang-orang yang pandai tidak merupakan himpunan sebab sifat “pandai” tidak dapat didefinisikan dengan tepat. Akibatnya tidak dapat ditentukan secara pasti apakah seseorang guru matematika termasuk dalam himpunan tersebut atau tidak. Kumpulan bunga yang harum juga bukan merupakan himpunan sebab penentuan harum tidaknya suatu bunga bersifat subjektif, maksudnya bunga yang dikategorikan harum oleh seseorang belum tentu dianggap harum bagi orang lain. Kumpulan lain bukan merupakan himpunan, misalnya

a. Kumpulan makanan enak,

b. Kumpulan wanita cantik, dan

c. Kumpulan lukisan indah.

Nama suatu himpunan biasanya menggunakan huruf kapital seperti A, B, C, dan X. Sedangkan anggota suatu himpunan biasanya dinotasikan dengan huruf kecil seperti a, b, c, x, dan y. Misalnya H adalah himpunan semua huruf hidup dalam alfabet Latin maka benda-benda yang termasuk dalam himpunan H adalah a, i, u, e, dan o. Benda-benda yang masuk dalam suatu himpunan disebut sebagai anggota himpunan tersebut. Notasi untuk menyatakan anggota suatu himpunan adalah “Δ sedangkan notasi untuk bukan anggota adalah “Ï”. Dengan demikian a Î H, iÎH, u Î H, e Î H, dan o Î H sedangkan b Ï H, c Ï H dan d ÏH. Istilah anggota yang digunakan di atas dapat diganti dengan istilah elemen atau unsur.

Dalam menyatakan suatu himpunan ada tiga cara, yakni dengan kalimat, dengan cara mendaftar, dan dengan notasi pembentuk himpunan. Cara mendaftar dilakukan dengan menuliskan anggota-anggotanya di dalam tanda tabulasi { } dimana antar anggota dibatasi dengan tanda koma. Sebagai contoh himpunan H = { a, i, u, e, o } menyatakan himpunan semua huruf hidup dalam alfabet Latin.

Himpunan X yang anggota-anggotanya memenuhi sifat P dinotasikan sebagai

X = { x | x bersifat P }.

Notasi ini disebut notasi pembentuk himpunan. Contoh dari notasi ini adalah H = { x | x adalah satu dari lima huruf hidup dalam alfabet Latin}. Tanda garis tegak “|” dapat diganti dengan tanda garis miring “ / ”, tanda bagi “ : “ atau tanda titik-koma “ ; “. Dalam buku matematika SMP tanda yang digunakan adalah tanda tegak “| ”.

Untuk memperjelas tentang berbagai cara menyatakan himpunan, perhatikan tiga contoh berikut yang menyatakan himpunan yang sama.

a. Himpunan semua bilangan genap positif.

b. { 2, 4, 6, 8, … }

c. { x | x = 2 n , n adalah bilangan asli}.

Masing-masing cara dalam menyatakan himpunan mempunyai kelebihan dan kelemahan masing-masing. Misalnya kelebihan cara mendaftar adalah apabila digunakan untuk himpunan yang sedikit anggotanya sedangkan kelemahannya adalah apabila digunakan untuk menulis himpunan yang anggota-anggotanya tidak berpola dan tidak mungkin didaftar semuanya. Sebagai contoh himpunan semua Warga Negara Indonesia tidak efisien bila ditulis dengan cara mendaftar.

Jenis himpunan dapat dibedakan berdasarkan banyaknya anggota himpunan tersebut. Himpunan dikatakan berhingga apabila mempunyai m anggota berbeda, dimana m suatu bilangan cacah. Selain itu disebut himpunan tak berhingga. Himpunan semua huruf dalam alfabet Latin, himpunan bilangan prima yang genap, dan himpunan semua bilangan asli kurang dari 1.000.000 adalah tiga contoh himpunan berhingga. Sedangkan himpunan bilangan ganjil dan himpunan bilangan real termasuk himpunan tak berhingga. Notasi n(H) digunakan untuk menyatakan bilangan kardinal himpunan H. Notasi tersebut adakalanya ditulis |H|. Jadi apabila H = {a, i, u, e,o} maka n(H) = 5, dan bila K = { 0 } maka n(K) = 1.

Misalkan himpunan I = { x | x Î [0, 1] } dan A adalah himpunan semua bilangan asli. Keduanya merupakan himpunan tak berhingga. Dalam hal ini n(I) = ¥ dan juga n(A) = ¥. Himpunan A merupakan himpunan terhitung (countable) karena kita dapat mengurutkan satu persatu anggota-anggotanya. Sedangkan himpunan I merupakan himpunan tak terhitung (uncountable). Akibatnya penulisan lambang ¥ di atas mempunyai kelemahan karena belum membedakan himpunan terhitung dan tak terhitung. Seorang matematikawan, Cantor, memberikan notasi yang lebih baik yakni n(A) = À₀ (dibaca aleph-nol) sedangkan n(I) = c. Simbol À (dibaca aleph ) merupakan huruf pertama dalam alfabet Hebrew.

Adakalanya suatu himpunan tidak memiliki anggota sama sekali. Himpunan seperti ini disebut sebagai himpunan kosong yang dinotasikan dengan { } atau simbol Æ. Tanda Æ merupakan huruf phi dalam alfabet Yunani. Contoh-contoh himpunan kosong adalah:

a. Himpunan semua anak Indonesia yang tingginya lebih dari 3 meter.

b. Himpunan semua bilangan ganjil yang habis dibagi 2.

c. { x | x² + 1 = 0, x adalah bilangan bulat}

d. { x | x² - 9 = 0, 2x - 4 = 0}

e. { x | x ¹ x }

f. H = { x | x Ï H}
Sifat Unsur-unsur himpunan 

Sifat keterikatan tertentu benda-benda didalam suatu himpunan disebut juga sifat himpunan, adapun sifat dari himpunan adalah

o  Objek di dalam suatu himpunan bisa dibedakan antara obyek satu dengan yang lainnya, misalnya himpunan hewan dalam hutan, dim ana anggotanya bisa harimau, jerapah, gajah dan sebagainya.

o  Unsur yang berada di dalam suatu himpunan dapat dibedakan dengan unsur yang tidak berada didalam ruangan.misalnya himpunan benda dalam aquarium bisa dibedakan dengan benda yang berada diluar aquarium, misalnya kursi yang ada diluar.

1.         Ciri-ciri Himpunan

a.    Adanya benda yang merupakan suatu anggota himpunan

b.    Adanya sejumlah unsur pembentuk himpunan

c.    Adanya unsur yang bukan termasuk anggota himpunan.

2.         Lambang Himpunan

Suatu himpunan dapat ditulis dengan lambang kurung kurawal pembuka ({ ) dan diakhiri dengan kurung kurawal penutup( } ). Himpunan selalu di beri nama dengan huruf kapital (huruf besar). Unsur-unsur yang termasuk dalam objek himpunan ditulis diantara tanda kurung kurawal.
Contohnya : himpunan X adalah himpunan bilangan prima kurang dari 20, ditulis X = {bilangan prima kurang dari 20}.

3.         Menyatakan Himpunan

 Ada tiga cara untuk menyatakan suatu himpunan:

a.    Mendaftar adalah suatu metode yang digunakan dengan cara menyebutkan anggotanya atu persatu. Contohnya X bilangan kurang dari 10.ditulis A = {1,2,3,4,5,6,7,8,9)

b.    Menggunakan notasi pembentukan himpunan,yaitu dengan menyatakan suatu himpunan dengan variabel dan menyatakan sifat-sifatnya. Contohnya B adalah suatu himpunan yang anggotanya bilangan genap. Ditulis B = {x/x adalah bilangan genap}

c.    Dengan menggunakan kata-kata yaitu dengan cara merangkai kata-kata yang mengambarkan suatu bilangan. Contohnya A adalah himpunan yang anggotanya adalah hewan berkaki empat. Ditulis A = {hewan kaki empat}

4.         Anggota Himpunan

Anggota himpuna disebut juga elemen himpunan. Anggota atau elemen himpunan adalah semua unsur yang terdapat di dalam suatu himpunan. Anggota suatu himpunan ditulis dengan menggunakan simbol “E”. Sedang kan yang bukan dilambangkan dengan E coret. Contohnya salah satu anggota atau elemen kurang dari 5 adalah {1,2,3,4}.

B2.   JENIS-JENIS HIMPUNAN

1.         himpunan berhingga adalah suatu himpunan yang jumlah anggotanya dapat dihitung. Contohnya D = {bilangan genap kurang dari 10} atau A = {2,4,6,8}. Himpunan D jumlah angotanya dapat dihitung yaitu sebanyak 4 buah.

2.         Himpunan tak hingga adalah suatu himpunan yang jumlah anggotanya tidak terbatas atau tak hingga. Contohnya: A= {bilangan genap}, B= {bilangan ganjil}

3.         Himpunan kosong adalah suatu himpunan yang tidak memiliki anggota sama sekali. Himpunan kosong dilambangkan dengan tanda {}. Contohnya B = {bilangan genap antara 2 dan 4}. ditulis B={}={0}.

4.         Himpunan equal/himpunan sama adalah himpunan yang anggotanya sama
contohnya A= {b,c,d}
B={d,c,b}
A=B

5.         Himpunan ekuivalen adalah himpunan-himpunan yang jumlah anggotanya sama.
Contohnya A= {b,c,d}
B={d,c,b}
A jumlahnya sama dengan B

6.         Himpunan semesta adalah himpunan dari semua unsur yang sedang dibicarakan. Himpunan semesta juga disebut himpunan uiversal dan ditulis dengan huruf S.
contohnya:
A = {1,3,5,7,9}
himpunan semestanya berupa:
S = {bilangan asli}
S = {bilangan cacah}
S = {bilangan ganjil kurang dari 10}

7.         Himpunan bagian adalah apabila setiap unsur dalam himpunan B termasuk juga anggota A, maka B merupakan bagian dari himpunan A.
contohnya
B = {a,c,e}
A = {a,b,c,d,e}
jadi B bagian dari A.

8.         Anggota himpunan n adalah suatu unsur dari suatu himpunan.
Contohnya
A = (a,b,c,d,e}
maka a elemen A

9.         Himpunan lepas adalah ssuatu himpunan yang tidak mempunyai anggota persekutuan dengan himpunan lain.
Contohnya
A = {d,e,f}
B = {g,h,i}
maka himpunan A tidak mempunyai anggota persekutuan dengan himpunan B atau A//B

10.     bukan anggota himpunan adalah unsur ini tidak termasuk dalam himpunan tersebut
contohnya
A = {a,b,c,d}
e bukan anggota himpunan A.

11.     Himpunan biolangan cacah adalah himpunan bilangan yang anggotanya dimulai dari nol dan seterusnya
contoh
K = {0,1,2,3,4,5}

12.     Himpunan bilangan asli adalah himpunan bilangan yang anggotanya dimulai dari bilangan satu dan seterusnya.
Contohnya
D = {1,2,3,4,}

13.     himpunan bilangan genap adalah himpunan yang anggotanya dimulai dari angka dua dan selalu genap atau habis dibagi dua
contohnya
G = {2,4,6,8,10}

14.     himpunan bilangan ganjil adalah himpunan yang anggota bilanganya tidak habis dibagi dua
contohnya
K = {1,3,5,7}

15.     himpunan blangan prima adalah himpunan bilangan yang anggotanya semua bilangan yang memiliki dua faktor
contohnya
Y = {2,3,,5,7}

16.     himpunan kuadrat bilangan cacah adalah himpunan bilangan cacah yang anggotanya dipangkatkan dua. Contohnya Y = {0^2,1^2,3^2)

3.     DIAGRAM VENN

Diagram venn adalah suatu gambar yang digunakan untuk menyatakan suatu himpunan dalam himpunan semesta. Ciri dari diagram venn adalah adanya bilangan asli dan himpunan semesta. Contohnya:

Buat diagram venn jika
S = { 1, 2, 3, 4, 5, 6, 7, 8 }
A = { 1, 4, 6, 7 }
B = { 2, 4, 5, 8 }

4.     OPERASI pada HIMPUNAN

1.         Irisan

Irisan adalah dua himpunan yang bagian-bagiannya menjadi anggota dari keduanya.

Contohnya: Irisan himpunan A dan B
A n B = { x | x A dan B }
Jika A = { 2, 7, 9, 11 }
Jika B = { 1, 5, 9, 10}
Maka A n B = 9

Atau

2.         Gabungan

Gabungan adalah dua himpunan yang anggotanya hanya bilangan itu saja misalnya anggota bilangan A saja, anggota bilangan B saja dan anggota A, B keduanya.

Contohnya: A u B = { x A, atau x B}
Jika A = { 5, 7, 9, 11 )
Jika B = { 6, 7, 8, 9, 10 }
A u B = { 5, 6, 7, 8, 9 10, 11 )

3.         Sifat-sifat operasi himpunan

         a. Komutatif

            1)   Irisan,     =>        Berlaku:                       A n B = B n A

            2)   Gabungan,          =>        Berlaku:                       A u B = B u A

b. Asosiatif

1)   Irisan tiga himpunan,      =>        (A n B) n C = A n ( B n C)

2)   Gabungan tiga himpunan,           =>        (A u B) u C = A u ( B u C)

c.    Distributif

1)   Irisan,     =>        A n ( B u C ) = (A n B) u (A n C)

2)   Gabungan,          =>        A u (B n C) = (A u B) n (A u C)

LATIHAN SOAL

1.       Dari sekelompok anak terdapat 15 anak gemar bulu tangkis, 20 anak gemar tenis meja, dan 12 anak gemar keduanya. Jumlah anak dalam kelompok tersebut adalah…

A.  17 orang

B.  23 orang

C.  35 orang

D.  47 orang

Penyelesaian :  ( B )

Diketahui :

n(A)          = 15

n(B)          = 20

n(A∩B)    = 12

Ditanya : n ( S )

Jawab :

 n(S)          =  n(A) + n(B) - n(A∩B)

                  = 15 + 20 – 12

                  = 23 .

2.       Dalam suatu kelas terdapat 47 siswa, setelah dicatat terdapat 38 anak senang berolahraga, 36 anak senang membaca, dan 5 orang anak tidak senang berolahraga maupun membaca. Banyak anak  yang senang berolahraga dan senang membaca adalah…

A.  28 anak

B.  32 anak

C.  36 anak

D.  38 anak

Penyelesaian : ( B )

Diketahui :

n(S)=  47 ;  n(O)= 38 ;  n(M)= 36 ;  n(X) = 5 (Tidak senang keduanya)

Ditanya : n(O∩M)

Jawab :

n(S)           =( n(O) + n(M) - n(O∩M) ) + n(X)

47              = (38 + 36 - n(O∩M) ) + 5

47 – 5        = 74 - n(O∩M)

42              = 74 - n(O∩M)

n(O∩M)    = 74 – 42 = 32.

Contoh Soal 1

Dalam penelitian yang dilakukan pada sekelompok orang, dipeoleh data 68 orang sarapan dengan nasi, 50 orang sarapan dengan roti, dan 8 orang sarapan nasi dan roti, sedangkan 35 orang sarapannya tidak dengan nasi ataupun roti. Hitung banyaknya orang dalam kelompok tersebut!

Jawab:

Kita gunakan diagram ven untuk menjawab soal tersebut. Jika kita gambarkan dengan diagram ven maka gambarnya seperti gambar berikut ini.

Banyak orang yang ada di dalam kelompok tersebut adalah 60 + 8 + 42 + 35 = 145 orang. Jadi, banyaknya orang dalam kelompok tersebut ada 145 orang.

Contoh Soal 2

Dari beberapa anak remaja diketahui 25 orang suka minum susu, 20 orang suka minum kopi dan 12 orang suka susu dan kopi. Dari data di atas jawablah pertanyaan di bawah ini.

a. jumlah semua anak remaja

b. jumlah remaja yang suka susu saja

c. jumlah remaja yang suka kopi saja

d. jumlah remaja yang suka kedua-duanya

Jawab:

Untuk menjawab soal tersebut Anda harus membuat data tersebut menjadi bentuk diagram ven. Jika digambarkan maka bentuk diagram vennya menjadi seperti gambar berikut ini.

Dari diagram venn di atas maka.

a. jumlah semua anak remaja = 33 orang

b. jumlah remaja yang suka susu saja = 13  orang

c. jumlah remaja yang suka kopi saja = 8 orang

d. jumlah remaja yang suka kedua-duanya = 12 orang

Contoh Soal 3

Hasil survey terhadap 35 orang penduduk di suatu desa, diperoleh hasil sebagai berikut: 18 orang menyukai teh, 17 orang menyukai kopi, 14 orang menyukai susu, 8 orang menyukai minum teh dan kopi, 7 orang menyukai teh dan susu, 5 orang menyukai kopi dan susu, 3 orang menyukai ketiga-tiganya. Buatlah diagram Venn dari keterangan di atas dan tentukan banyaknya warga menyukai teh, menyukai susu, menyukai kopi, dan tidak menyukai ketiga-tiganya.

Jawab:

Diagram Venn dari keterangan di atas seperti gambar berikut ini.

Dari diagram venn di atas maka banyaknya warga yang gemar minum teh saja ada 6 orang, gemar minum susu saja ada 5 orang, gemar minum kopi saja ada 7 orang  dan tidak gemar ketiga-tiganya ada 3 orang.

Contoh Soal 4

Jika diketahui banyaknya kepala keluarga dari warga RT 02 adalah 75 orang. Di antara kepala keluarga ini yang berlangganan koran ada 50 orang, yang berlangganan majalah ada 25 orang, yang berlangganan majalah dan koran ada 10 orang. Dengan menggunakan bantuan diagram Venn, tentukan banyaknya kepala keluarga dari warga RT 02 yang tidak berlangganan keduanya!

Jawab:

Jika digambarkan maka bentuk diagram vennya menjadi seperti gambar berikut ini.

Berdasarkan gambar diagram venn di atas maka banyaknya kepala keluarga dari warga RT 02 yang tidak berlangganan keduanya ada 10 orang.

Contoh Soal 5

Perhatikan diagram Venn berikut.

Misalkan S = Himpunan siswa di kelasmu

M= Himpunan siswa yang menyukai matematika

B = Himpunan siswa yang menyukai bahasa Inggris

K = Himpunan siswa yang menyukai kesenian

Jika setiap siswa diwakili oleh sebuah titik, maka tentukan:

a. berapa orang siswa yang menyukai matematika?

b. berapa orang siswa yang menyukai matematika dan kesenian?

c. berapa orang yang menyukai bahasa Inggris tetapi tidak menyukai kesenian?

d. berapa orang siswa yang menyukai ketiga-tiganya?

e. berapa orang yang hanya menyukai kesenian saja?

f. berapa orang yang menyukai matematika dan bahasa Inggris tetapi tidak menyukai kesenian?

g. berapa orang yang tidak menyukai ketiga-tiganya?

h. berapa orang yang hanya menyukai salah satu dari ketiga pelajaran tersebut?

Jawab:

a. siswa yang menyukai matematika ada 7 orang (daerah yang diarsir cokelat merupakan daerah yang suka matematika), seperti gambar berikut ini.

b. Siswa yang menyukai menyukai matematika dan kesenian ada 1 orang (daerah yang diarsir biru merupakan daerah yang suka matematika dan kesenian) seperti gambar berikut ini.

c. Siswa yang menyukai menyukai bahasa Inggris tetapi tidak menyukai kesenian ada 5 orang (daerah yang diarsir kuning merupakan daerah yang suka bahasa Inggris tetapi tidak menyukai kesenian) seperti gambar berikut ini.

d. Siswa yang menyukai ketiga-tiganya ada 1 orang (daerah yang diarsir merah merupakan daerah yang suka ketiga-tiganya), seperti gambar berikut ini.

e. Siswa yang menyukai kesenian saja ada 2 orang (daerah yang diarsir merah muda merupakan daerah yang suka kesenian saja), seperti gambar berikut ini.

f. Siswa yang menyukai menyukai matematika dan bahasa Inggris tetapi tidak menyukai kesenian ada 8 orang (daerah yang diarsir hijau merupakan daerah yang suka matematika dan bahasa Inggris tetapi tidak menyukai kesenian) seperti gambar berikut ini.

g. orang yang tidak menyukai ketiga-tiganya ada 8 orang (yang berada di luar lingkaran merupakan daerah yang tidak suka ketiga-tiganya)

h. Jumlah orang yang hanya menyukai salah satu dari ketiga pelajaran tersebut ada 8 orang (daerah yang diarsir merah tua merupakan daerah yang hanya menyukai salah satu dari ketiga pelajaran tersebut) seperti gambar berikut ini.

Sumber : http://mafia.mafiaol.com/2013/01/contoh-soal-penerapan-himpunan-dalam.html

http://inilycca.blogspot.com/2011/09/soal-soal-dan-pembahasan-materi.html

http://himpunan-matematika.blogspot.com/